Dealing with non-normal data – Generalized Linear Models
As you remember, when we first introduced the simple linear
model (Linear Models in Agriculture) we defined a set of assumptions that need to be met to apply this model.
In the same post, we talked about methods to deal with deviations from assumptions of
independence, equality of variances and balanced designs and the fact that,
particularly if our dataset is large, we may reach robust results even if our
data are not perfectly normal. However, there are datasets for which the target
variable has a completely different distribution from the normal, this means that also the error terms will not be normally distributed.
In these cases we need to change our modelling method and employ generalized linear models (GLM). Common scenarios where GLM should be considered are studies where the variable of interest is binary, for example presence or absence of a species, or where we are interested in modelling counts, for example the number of insects present in a particular location. In these cases, where the target variable is not continuous but rather discrete or categorical, the assumption of normality is usually not met. In this section we will focus on the two scenarios mentioned above, but GLM can be used to deal with data distributed in many different ways, and we will introduce how to deal with more general cases.
In these cases we need to change our modelling method and employ generalized linear models (GLM). Common scenarios where GLM should be considered are studies where the variable of interest is binary, for example presence or absence of a species, or where we are interested in modelling counts, for example the number of insects present in a particular location. In these cases, where the target variable is not continuous but rather discrete or categorical, the assumption of normality is usually not met. In this section we will focus on the two scenarios mentioned above, but GLM can be used to deal with data distributed in many different ways, and we will introduce how to deal with more general cases.
Count Data
Data of this type, i.e. counts or rates, are characterized
by the fact that their lower bound is always zero. This does not fit well with
a normal linear model, where the regression line may well estimate negative
values. For this type of variable we can employ a Poisson Regression, which fits
the following model:
As you can see the equation is very
similar to the standard linear model, the difference is that to insure that all
Y are positive (since we cannot have negative values for count data) we are
estimating the log of Y. This is referred to as the link function, meaning the transformation of y that we need to make to insure linearity of the response. For the model we are going to look at below, which are probably the most common, the link function is implicitly called, meaning that glm call the right function for us and we do not have to specify it explicitly. However, we can do that if needed.
From this equation you may think that instead of using glm we could log transform y and run a normal lm. The problem with that would be that lm is assuming a normal error term with constant variance (as we saw with the plot fitted versus residuals), but for this model this assumption would be violated. That is why we need to use glm.
From this equation you may think that instead of using glm we could log transform y and run a normal lm. The problem with that would be that lm is assuming a normal error term with constant variance (as we saw with the plot fitted versus residuals), but for this model this assumption would be violated. That is why we need to use glm.
In R fitting this model is very easy. For
this example we are going to use another dataset available in the package agridat, named beall.webworms,
which represents counts of webworms in a beet field, with insecticide
treatments:
> dat = beall.webworms
> str(dat)
'data.frame': 1300 obs. of 7 variables:
$ row : int 1 2 3 4 5 6 7 8 9 10 ...
$ col : int 1 1 1 1 1 1 1 1 1 1 ...
$ y : int 1 0 1 3 6 0 2 2 1 3 ...
$ block: Factor w/ 13 levels "B1","B10","B11",..: 1 1 1 1 1 6 6 6 6 6 ...
$ trt : Factor w/ 4 levels "T1","T2","T3",..: 1 1 1 1 1 1 1 1 1 1 ...
$ spray: Factor w/ 2 levels "N","Y": 1 1 1 1 1 1 1 1 1 1 ...
$ lead : Factor w/ 2 levels "N","Y": 1 1 1 1 1 1 1 1 1 1 ...
We can check the distribution of our data with the function hist:
hist(dat$y, main="Histogram of Worm Count", xlab="Number of Worms")
We are going to fit a simple model first to see how to
interpret its results, and then compare it with a more complex model:
pois.mod = glm(y ~ trt, data=dat, family=c("poisson"))
As you can see the model features a new option called family, here you specify the distribution of the error term, in this case a poisson distribution. We should also specify a log link function as we saw before, but this is the default setting so there is no need to include it.
Once again the function summary will show some useful details about this model:
Once again the function summary will show some useful details about this model:
> summary(pois.mod)
Call:
glm(formula = y ~ trt, family = c("poisson"), data = dat)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6733 -1.0046 -0.9081 0.6141 4.2771
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.33647 0.04688 7.177 7.12e-13 ***
trtT2 -1.02043 0.09108 -11.204 < 2e-16 ***
trtT3 -0.49628 0.07621 -6.512 7.41e-11 ***
trtT4 -1.22246 0.09829 -12.438 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1955.9 on 1299 degrees of freedom
Residual deviance: 1720.4 on 1296 degrees of freedom
AIC: 3125.5
Number of Fisher Scoring iterations: 6
Update 08/12/2017
Note on interpretation
To interpret the coefficients of the model we need to remember that this GLM uses a log link function. Therefore for example the -1.02 is log transformed, so the coefficient for T2 would be exp(-1.02)=0.36.
In terms of interpretation, we can say that the number of worms for T2 is 0.36 times the number of worms for T1 (this is because the coefficient is always referred to the reference level). So there is a decrease, and that is why the coefficient is negative.
More info here: https://stats.stackexchange.com/questions/234057/interpretation-of-slope-estimate-of-poisson-regression
The first valuable information is related to the residuals of the model, which should be symmetrical as for any normal linear model. From this output we can see that minimum and maximum, as well as the first and third quartiles, are similar, so this assumption is confirmed. Then we can see that the variable trt (i.e. treatment factor) is highly significant for the model, with very low p-values. The statistical test in this case is not a t-test, as in the output of the function lm, but a Wald Test (Wald Test). This test computes the probability that the coefficient is 0, if the p is significant it means the chances the coefficient is zero are very low so the variable should be included in the model since it has an effect on y.
Another important information is the deviance, particularly the residual deviance. As a general rule, this value should be lower or in line than the residuals degrees of freedom for the model to be good. In this case the fact that the residual deviance is high (even though not dramatically) may suggests the explanatory power of the model is low. We will see below how to obtain p-value for the significance of the model.
We can use the function plot to obtain more info about how the model fits our data:
par(mfrow=c(2,2))
plot(pois.mod)
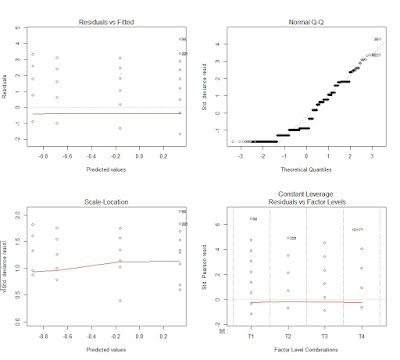
This creates the following plot, where the four outputs are included in the same image:
This plots tell a lot about the goodness of fit of the model. The first image in top left corner is the same we created for lm (i.e. residuals versus fitted values). This again does not show any trend, just a general underestimation. Then we have the normal QQ plot, where we see that the residuals are not normal, which violates one of the assumptions of the model. Even though we are talking about non-linear error term, we are "linearizing" the model with the link function and by specifying a different family for the error term. Therefore, we still need to obtain normal residuals.
The effects of the treatments are all negative and referred to the first level T1, meaning for example that a change from T1 to T2 will decrease the count by 1.02. We can check this effect by estimating changes between T1 and T2 with the function predict, and the option newdata:
> predict(pois.mod, newdata=data.frame(trt=c("T1","T2")))
1 2
0.3364722 -0.6839588
Another important piece of information are the Null and
Residuals deviances, which allow us to compute the probability that this model
is better than the Null hypothesis, which states that a constant (with no
variables) model would be better.
We can compute the p-value of the model with the following line:
We can compute the p-value of the model with the following line:
> 1-pchisq(deviance(pois.mod), df.residual(pois.mod))
[1] 1.709743e-14
This p-value is very low, meaning that this model fits the
data well. However, it may not be the best possible model, and we can use the
AIC parameter to compare it to other models. For example, we could include more
variables:
pois.mod2 = glm(y ~ block + spray*lead, data=dat, family=c("poisson"))
How does this new model compare with the previous?
> AIC(pois.mod, pois.mod2)
df AIC
pois.mod 4 3125.478
pois.mod2 16 3027.438
As you can see the second model has a lower AIC, meaning
that fits the data better than the first.
One of the assumptions of the Poisson distribution is that
its mean and variance have the same value. We can check by simply comparing
mean and variance of our data:
> mean(dat$y)
[1] 0.7923077
> var(dat$y)
[1] 1.290164
In cases such as this when the variance is larger than the
mean (in this case we talk about overdispersed count data) we should employ
different methods, for example a quasipoisson distribution:
pois.mod3 = glm(y ~ trt, data=dat, family=c("quasipoisson"))
The summary function provides us with the dispersion
parameter, which for a Poisson distribution should be 1:
> summary(pois.mod3)
Call:
glm(formula = y ~ trt, family = c("quasipoisson"), data = dat)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6733 -1.0046 -0.9081 0.6141 4.2771
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.33647 0.05457 6.166 9.32e-10 ***
trtT2 -1.02043 0.10601 -9.626 < 2e-16 ***
trtT3 -0.49628 0.08870 -5.595 2.69e-08 ***
trtT4 -1.22246 0.11440 -10.686 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for quasipoisson family taken to be 1.35472)
Null deviance: 1955.9 on 1299 degrees of freedom
Residual deviance: 1720.4 on 1296 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 6
Since the dispersion parameter is 1.35, we can conclude that
our data are not terrible overdispersed, so maybe a Poisson regression would still
be appropriate for this dataset.
The we run the following line, which test whether the dispersion parameter is higher than 1, which is the assumption for the Poisson regression:
As you can see the alternative hypothesis is that the dispersion parameter is higher than 1. Since the p-value is very low we can accept this alternative hypothesis and therefore use other forms of modelling. Since the dispersion is still close to 1, I think we can use the quasipoisson family. However, if this was higher it would have been better to use the negative binomial family with the function glm.nb in the package MASS, see below.
Another way of directly comparing the two models is with the analysis of deviance, which can be performed with the function anova:
This test compares the residual deviance of the two models to see whether they are different and calculates a p-values. In this case the p-value is highly significant, meaning that the models are different. Since we already compared the AIC, we can conclude that pois.mod2 is significantly (low p-value) better (lower AIC) than pois.mod.
Update 28/07/2017 - Overdispersion Test
In the package AER there is a function to directly test for overdispersion. The procedure to do so is quite simple:
First of all we install the package:
install.packages("AER")
library(AER)
The we run the following line, which test whether the dispersion parameter is higher than 1, which is the assumption for the Poisson regression:
> dispersiontest(pois.mod, alternative="greater")
Overdispersion test
data: pois.mod
z = 6.0532, p-value = 7.101e-10
alternative hypothesis: true dispersion is greater than 1
sample estimates:
dispersion
1.350551
As you can see the alternative hypothesis is that the dispersion parameter is higher than 1. Since the p-value is very low we can accept this alternative hypothesis and therefore use other forms of modelling. Since the dispersion is still close to 1, I think we can use the quasipoisson family. However, if this was higher it would have been better to use the negative binomial family with the function glm.nb in the package MASS, see below.
Another way of directly comparing the two models is with the analysis of deviance, which can be performed with the function anova:
> anova(pois.mod, pois.mod2, test="Chisq")
Analysis of Deviance Table
Model 1: y ~ trt
Model 2: y ~ block + spray * lead
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 1296 1720.4
2 1284 1598.4 12 122.04 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
This test compares the residual deviance of the two models to see whether they are different and calculates a p-values. In this case the p-value is highly significant, meaning that the models are different. Since we already compared the AIC, we can conclude that pois.mod2 is significantly (low p-value) better (lower AIC) than pois.mod.
However, there are cases where the data are very overdispersed. In those cases, when we see that the distribution has lots of peaks we need to employ the negative binomial regression, with the function glm.nb available in the package MASS:
library(MASS)
NB.mod1 = glm.nb(y ~ trt, data=dat)
NOTE:
For GLM it is possible to also compute pseudo R-Squared to ease the interpretation of their accuracy. This can be done with the function pR2 from the package pscl. Please read below (Logistic Regression section) for an example on the use of this function.
Logistic Regression
Another popular form of regression that can be tackled with
GLM is the logistic regression, where the variable of interest is binary (0 or 1, presence or absence and any other binary outcome). In this case the
regression model takes the following equation:
Again, the equation is identical to the
standard linear model, but what we are computing from this model is the log of
the probability that one of the two outcomes will occur, also referred as logit function.
Update 07/02/2018
By reviewing some literature I realized that the term logistic regression can be confusing. Sometimes it is used indistinctly to indicate both model with a binary outcome, and models that involve proportions. However, this is probably not totally correct because binary outcome follow a Bernoulli distribution, and in such cases we should probably talk about Bernoulli regression. In R there is no distinction between the two, and both models can be fitted with the option family="binomial", but in other software there is, e.g. Genstat. In Genstat to run a regression with binary outcome you would select a Bernoulli distribution, while for proportions you would select a Binamial distribution.
In regards to the link function, even though the logit is probably the most commonly used, some authors also employ the probit transformation. According to Geyer (2003, http://www.stat.umn.edu/geyer/5931/mle/glm.pdf) but are legitimate transformations and they should not differ much in terms of fitting. The regression coefficient would be different when using the probit compared to the logit. However, if we use the function predict (as suggested here) and we do not rely on the coefficient, we should come up with very similar solutions.
For this example we are going to use another
dataset available in the package agridat
called johnson.blight,
where the binary variable of interest is the presence or absence of blight
(either 0 or 1) in potatoes:
> dat = johnson.blight
> str(dat)
'data.frame': 25 obs. of 6 variables:
$ year : int 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 ...
$ area : int 0 0 0 0 50 810 120 40 0 0 ...
$ blight : int 0 0 0 0 1 1 1 1 0 0 ...
$ rain.am : int 8 9 9 6 16 10 12 10 11 8 ...
$ rain.ja : int 1 4 6 1 6 7 12 4 10 9 ...
$ precip.m: num 5.84 6.86 47.29 8.89 7.37 ...
In R fitting this model is very easy. In this case we are trying to see if the presence of blight is related to the number of rainy days in April and May (column rain.am):
mod9 = glm(blight ~ rain.am, data=dat, family=binomial)
we are now using the binomial distribution for a logistic
regression. To check the model we can rely again on summary:
> summary(mod9)
Call:
glm(formula = blight ~ rain.am, family = binomial, data = dat)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.9395 -0.6605 -0.3517 1.0228 1.6048
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.9854 2.0720 -2.406 0.0161 *
rain.am 0.4467 0.1860 2.402 0.0163 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 34.617 on 24 degrees of freedom
Residual deviance: 24.782 on 23 degrees of freedom
AIC: 28.782
Number of Fisher Scoring iterations: 5
This table is very similar to the one created for count
data, so a lot of the discussion above can be used here. The main difference is
in the way we can interpret the coefficients, because we need to remember that
here we are calculating the logit function of the probability, so 0.4467
(coefficient for rain.am) is not the actual probability associated with an
increase in rain. However, what we can say by just looking at the coefficients
is that rain has a positive effect on blight, meaning that more rain increases
the chances of finding blight in potatoes.
To estimate probabilities we need to use the function
predict (we could do it manually: Logistic Regression but this is easier):
> predict(mod9, type="response")
1 2 3 4 5 6 7
0.19598032 0.27590141 0.27590141 0.09070472 0.89680283 0.37328295 0.59273722
8 9 10 11 12 13 14
0.37328295 0.48214935 0.19598032 0.69466455 0.19598032 0.84754431 0.27590141
15 16 17 18 19 20 21
0.93143346 0.05998586 0.19598032 0.05998586 0.84754431 0.59273722 0.59273722
22 23 24 25
0.48214935 0.59273722 0.98109229 0.89680283
This calculates the probability associated with the values
of rain in the dataset. To know the probability associated with new values of
rain we can again use predict with the option newdata:
>predict(mod9,newdata=data.frame(rain.am=c(15)),type="response")
1
0.8475443
This tells us that when rain is equal to 15 days between April and May, we have 84%
chances of finding blight (i.e. chances of finding 1) in potatoes.
We could use the same method to compute probabilities for a series of values of rain to see what is the threshold of rain that increases the probability of blight above 50%:
As you can see we are using once again the function predict, but in this case we are estimating the probabilities for increasing values of rain. Then we are plotting the results:
From this plot it is clear that we reach a 50% probability at around 12 rainy days between April and May.
which creates the following plot:
We could use the same method to compute probabilities for a series of values of rain to see what is the threshold of rain that increases the probability of blight above 50%:
prob.NEW = predict(mod9,newdata=data.frame(rain.am=1:30),type="response")
plot(1:30, prob.NEW, xlab="Rain", ylab="Probability of Blight")
abline(h=0.5)
As you can see we are using once again the function predict, but in this case we are estimating the probabilities for increasing values of rain. Then we are plotting the results:
From this plot it is clear that we reach a 50% probability at around 12 rainy days between April and May.
Update 26/07/2017
Another simpler way to create the plot above would be with the function plotPredy, in the package rcompanion: install.packages("rcompanion")
library(rcompanion)
plotPredy(data = dat,
y = blight,
x = rain.am,
model = mod9,
type = "response",
xlab = "Rain",
ylab = "Blight")
which creates the following plot:
To assess the accuracy of the model we can use two
approaches, the first is based on the deviances listed in the summary. The
Residual deviance compares this model with the one that fits the data
perfectly. So if we calculate the following p-value (using the deviance and df
in the summary table for residuals):
> 1-pchisq(24.782, 23)
[1] 0.3616226
We see that because it is higher than 0.05 we cannot reject
that this model fits the data as well as the perfect model, therefore our model
seems to be good.
We can repeat the same procedure for the Null hypothesis,
which again tests whether this model fits the data well:
> 1-pchisq(34.617, 24)
[1] 0.07428544
Since this is again not significant it suggests (contrary to
what we obtained before) that this model is not very good.
An additional and probably easier to understand way to
assess the accuracy of a logistic model is calculating the pseudo R2, which can
be done by installing the package pscl:
install.packages("pscl")
library(pscl)
Now we can run the following function:
> pR2(mod9)
llh llhNull G2 McFadden r2ML r2CU
-12.3910108 -17.3086742 9.8353268 0.2841155 0.3252500 0.4338984
From this we can see that our model explains around 30-40% of
the variation in blight, which is not particularly good. We can use this index
to compare models, as we did for AIC.
Each of these R squared is computed in a different way and you can read the documentation to know more. In general, one of the most commonly reported is the McFadden, which however tends to be conservative, and the r2ML. In this paper you can find a complete overview/comparison of various pseudo R-Squared: http://www.glmj.org/archives/articles/Smith_v39n2.pdf
We can load the dataset crowder.seeds from agridat. In here the variable germ is the number of seeds that germinated, while n is the total number of seeds. Thus, we can obtain the proportion of seeds that germinated and we can try to model it.
The syntax to do so is the following:
Each of these R squared is computed in a different way and you can read the documentation to know more. In general, one of the most commonly reported is the McFadden, which however tends to be conservative, and the r2ML. In this paper you can find a complete overview/comparison of various pseudo R-Squared: http://www.glmj.org/archives/articles/Smith_v39n2.pdf
Update 26/07/2017
In the package rcompanion there is the function nagelkerke, which computes other pseudo R squared, like McFadden, Cox and Snell and Nagelkerke: > nagelkerke(mod9)
$Models
Model: "glm, blight ~ rain.am, binomial, dat"
Null: "glm, blight ~ 1, binomial, dat"
$Pseudo.R.squared.for.model.vs.null
Pseudo.R.squared
McFadden 0.284116
Cox and Snell (ML) 0.325250
Nagelkerke (Cragg and Uhler) 0.433898
$Likelihood.ratio.test
Df.diff LogLik.diff Chisq p.value
-1 -4.9177 9.8353 0.0017119
Update 26/07/2016 - Proportions
Proportions are generally in the range between 0 and 1, and so they may fit in the binomial family. In fact, one way of modelling proportion is to use the same glm code we saw for the logistic regression.
Let's look at one example:
> data = crowder.seeds
> str(data)
'data.frame': 21 obs. of 5 variables:
$ plate : Factor w/ 21 levels "P1","P10","P11",..: 1 12 15 16 17 18 19 20 21 2 ...
$ gen : Factor w/ 2 levels "O73","O75": 2 2 2 2 2 1 1 1 1 1 ...
$ extract: Factor w/ 2 levels "bean","cucumber": 1 1 1 1 1 1 1 1 1 1 ...
$ germ : int 10 23 23 26 17 8 10 8 23 0 ...
$ n : int 39 62 81 51 39 16 30 28 45 4 ...
The syntax to do so is the following:
> mod1 = glm(cbind(germ, n) ~ gen + extract, data=data, family="binomial")
> summary(mod1)
Call:
glm(formula = cbind(germ, n) ~ gen + extract, family = "binomial",
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5431 -0.5006 -0.1852 0.3968 1.4796
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.0594 0.1326 -7.989 1.37e-15 ***
genO75 0.1128 0.1311 0.860 0.39
extractcucumber 0.5232 0.1233 4.242 2.22e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 33.870 on 20 degrees of freedom
Residual deviance: 14.678 on 18 degrees of freedom
AIC: 104.65
Number of Fisher Scoring iterations: 4
Notice the use of cbind within the formula to calculate proportions.
Another technique you could use when dealing with proportions is the beta-regression. This can be fitted with the function betareg, in the package betareg. You can find more info at the following links:
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.473.8394&rep=rep1&type=pdf
A good tutorial on beta regression written by Salvatore S. Mangiafico can be found here:
http://rcompanion.org/handbook/J_02.html
The sample code to perform a beta regression on these data is the following:
I had to transform the proportion first using a correction suggested here https://stackoverflow.com/questions/26385617/proportion-modeling-betareg-errors
This is because one sample had value 0, and betareg does not work with either values 0 or 1.
Another technique you could use when dealing with proportions is the beta-regression. This can be fitted with the function betareg, in the package betareg. You can find more info at the following links:
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.473.8394&rep=rep1&type=pdf
A good tutorial on beta regression written by Salvatore S. Mangiafico can be found here:
http://rcompanion.org/handbook/J_02.html
The sample code to perform a beta regression on these data is the following:
#Beta-Regression
y.transf.betareg <- function(y){
n.obs <- sum(!is.na(y))
(y * (n.obs - 1) + 0.5) / n.obs
}
y.transf.betareg(data$germ/data$n)
mod2 = betareg(y.transf.betareg(data$germ/data$n) ~ gen + extract, data=data)
summary(mod2)
I had to transform the proportion first using a correction suggested here https://stackoverflow.com/questions/26385617/proportion-modeling-betareg-errors
This is because one sample had value 0, and betareg does not work with either values 0 or 1.
Dealing with other distributions and transformation
As mentioned, GLM can be used for fitting linear models not
only in the two scenarios we described above, but in any occasion where data do
not comply with the normality assumption. For example, we can look at another
dataset available in agridat, where the variable of interest is slightly
non-normal:
> dat = hughes.grapes
> str(dat)
'data.frame': 270 obs. of 6 variables:
$ block : Factor w/ 3 levels "B1","B2","B3": 1 1 1 1 1 1 1 1 1 1 ...
$ trt : Factor w/ 6 levels "T1","T2","T3",..: 1 2 3 4 5 6 1 2 3 4 ...
$ vine : Factor w/ 3 levels "V1","V2","V3": 1 1 1 1 1 1 1 1 1 1 ...
$ shoot : Factor w/ 5 levels "S1","S2","S3",..: 1 1 1 1 1 1 2 2 2 2 ...
$ diseased: int 1 2 0 0 3 0 7 0 1 0 ...
$ total : int 14 12 12 13 8 9 8 10 14 10 ...
The variable total presents a skewness of 0.73, which means
that probably with a transformation it should fit with a normal distribution.
However, for the sake of the discussion we will assume it cannot be
transformed. So now our problem is identify the best distribution for our data,
to do so we can use the function descdist in the package fitdistrplus we
already loaded:
descdist(dat$total, discrete = FALSE)
this returns the following plot:
Where we can see that our data (blue dot) are close to
normal and maybe closer to a gamma distribution. So now we can further check
this using another function from the same package:
plot(fitdist(dat$total,distr="gamma"))
which creates the following plot:
From this we can see that in fact our data seem to be close
to a gamma distribution, so now we can proceed with modelling:
mod8 = glm(total ~ trt * vine, data=dat, family=Gamma(link=identity))
in the option family we included the name of the
distribution, plus a link function that is used if we want to transform our
data (in this case the function identity is for leaving data not transformed).
This is what we do to model other types of data that do not
fit with a normal distribution. Other possible families supported by GLM are:
binomial, gaussian, Gamma, inverse.gaussian, poisson, quasi,
quasibinomial, quasipoisson
Other possible link functions (which availability depends on
the family) are:
logit, probit, cauchit, cloglog, identity, log, sqrt,
1/mu^2, inverse.
Generalized Linear Mixed Effects models
As linear model, linear mixed effects model need to comply
with normality. If our data deviates too much we need to apply the generalized
form, which is available in the package lme4:
install.packages("lme4")
library(lme4)
For this example we will use
again the dataset johnson.blight:
dat = johnson.blight
Now we can fit a GLME model with random effects for area,
and compare it with a model with only fixed effects:
mod10 = glm(blight ~ precip.m, data=dat, family="binomial")
mod11 = glmer(blight ~ precip.m + (1|area), data=dat, family="binomial")
> AIC(mod10, mod11)
df AIC
mod10 2 37.698821
mod11 3 9.287692
As you can see this new model reduces the AIC substantially.
The same function can be used for Poisson regression, but it does not work for quasipoisson overdispersed data. However, within lme4 there is the function glmer.nb for negative binomial mixed effect. The syntax is the same as glmer, except that in glmer.nb we do not need to include family.






No comments:
Post a Comment
Note: only a member of this blog may post a comment.